1- تقارن محوری
2- تقارن مرکزی
3- دوران
تقارن 90 درجه و 180 درجه نداریم
دوران 90 و 180 و هر زاویه دیگه داریم
تقارن یا نسبت به یک خط است یا نسبت به یک نقطه
نسبت به خط تقارن محوری
نسبت به نقطه تقارن مرکزی که حالتی از دوران است با چرخش 180 درجه
طبق تعریف هرگاه شکلی را نسبت به یک نقطه از خود شکل به اندازه 180 درجه دوران بدهیم و شکل بر روی خودش منطبق شود دارای مرکز تقارن هست و شکل مرکز تقارن دارد
-تقارن محوری:درتقارن محوری قرینه یک نقطه را نسبت به یک خط بدست می آوریم.
تقارن محوری خطی است که از هر نقطه شکل خطی به ان عمود کنیم و به همان اندازه امتداد بدهیم قرینه شکل به دست می اید.
بهترین حالت برای تقارن محوری تا کردن کاغذیه که در یه طرفش شکلی کشیدیم و بعد از تا کردن همان شکل را کپی می کنیم
محور تقارن:خطی است که قرینه هر نقطه ازشکل نسبت به آن برخود شکل منطبق می شود.یا خطی است که شکل را به دوقسمت مساوی تقسیم می کند.
-تقارن مرکزی:درتقارن مرکزی قرینه یک شکل را نسبت به یک نقطه بدست می آوریم.که آن نقطه مرکز تقارن شکل است.
در دوران، هر نقطه از شکل را نسبت به یک نقطه مشخص به اندازه زاویه موردنظر دوران میدهیم
دوران: صفر تا 360 درجه
صفر تا 180 درجه:تقارن چرخشی
180 درجه:تقارن مرکزی
مربع علاوه بر تقارن مرکزی تقارن چرخشی نیز دارد
مثلث متساوی الاضلاع تقارن مرکزی ندارد ولی تقارن چرخشی دارد
شش ضلعی منتظم هم تقارن مرکزی دارد هم تقارن چرخشی
پس اگر شکلی در 180 درجه روی خودش منطبق شود تقارن مرکزی دارد و اگر کمتر از 180 درجه روی خودش بیفتد تقارن چرخشی
تبدیل یافته هر شکل در تقارن محوری با آن شکل برابر است.
اما تساوی، تساوی معکوس است. زیرا طرز قرار گرفتن زاویه ها و راس های نظیر در دو شکل هندسی در دو جهت مختلف است.
نتیجه ترکیب دو تقارن با محورهای موازی یک انتقال است.
مرکزتقارن نقطه ای است که قرینه هرنقطه ازشکل نسبت به آن برخودشکل منطبق می شود.
مرکز تقارن نقطه ای درون شکل است که اگر هر نقطه از شکل را به ان متصل کنیدوبه همان اندازه درهمان راستا ادامه دهید نقطه ای روی شکل به دست می اید.
یعنی قرینه هر نقطه شکل نسبت به مرکز تقارن روی خود شکل قرار می گیرد.
دردو شکل زیر نقطه Oمرکز تقارن است. زیرا نقاط B1و Bنسبت به o روی شکل است.
در شکل های زیرO مرکز تقارن نیست. زیرا قرینه A نسبت به oروی خود شکل قرار ندارد.
به عبارت دیگر مرکز تقارن شکل، نقطه ای درون شکل است که اگر شکل را حول ان نقطه 180 درجه دوران دهیم بر خودش منطبق شود.مثال:نقطه oدر شکل مقابل(مستطیل)مرکز تقارن است زیرا اگر مستطیل را حول نقطه o180 درجه دروران دهیم برشکل اولیه منطبق می شود.در چند ضلعی های منتظم اگر تعداد ضلع ها زوج باشد مرکز تقارن دارنداگر تعداد ضلع ها فرد باشد مرکز تقارن ندارند.مثلث متساوی الاضلاع و 5 ضلعی مرکز تقارن ندارند.ولی مربع و 6 صلعی و10 ضلعی منتظم مرکز تقارن دارنددر مربع ومستطیل ولوزی و چند ضلعی های منتظم با تعداد ضلع زوج محل برخورد قطرها همان مرکز تقارن است.در شکل زیر oمرکز تقارن است زیرا هر نقطه مثل A و B را به o وصل کنیم به همان اندازه ادامه دهید نقاطی روی شکل به دست می اید.در شکل زیر oمرکز تقارن است زیرا هر نقطه مثل A و B را به o وصل کنیم به همان اندازه ادامه دهید نقاطی روی شکل به دست می اید.

مربع 4تا محور تقارن دارد. مستطیل دوتا محور تقارن دارد. لوزی 2تا محورتقارن دارد. متوازی الاضلاع محور تقارن ندارد. دایره بی شمار محور تقارن دارد.
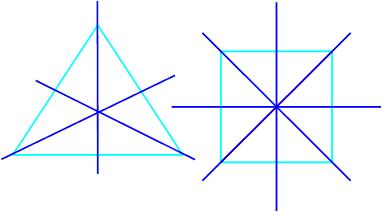
مثلث متساوی الاضلاع 3تا محورتقارن دارد.
مثلث متساوی الساقین یک محور تقارن دارد.
ذوزنقه متساوی الساقین یک محور تقارن دارد.
در هر یک از موارد زیر تعداد محورتقارن و مرکز تقارن درصورت وجود مشخص کنید.
الف)نقطه:یک مرکز تقارن دارد و آن خودش است، وبی شمار محور تقارن دارد.
ب)خط:بی شمار مرکزتقارن دارد،کلیه نقاطی که روی خط قرار دارند. بی شمار محور تقارن دارد.خطوطی که بر این نقاط می گذرند،
ج)nضلعی منتظم:nمحور تقارن دارد،اگر nزوج باشدیک مرکز تقارن دارد،واگرnفردباشدمرکز تقارن ندارد.
د)نیم خط: نیم خط مرکز تقارن ندارد،ولی یک محور تقارن دارد.
ه)پاره خط:دومحور تقارن عمودبرهم دارد،یکی عمود منصف آن ودیگری خطی است که پاره خط جزیی ازآن است.ویک مرکز تقارن دارد.
نکته 1: ذوزنقه ها درحالت کلی محورتقارن ندارند.
نکته 2: یک مثلث درحالت کلی محورتقارن ومرکزتقارن ندارد.
نکته3: مثلث متساوی الساقین مرکزتقارن ندارد.
نکته4: مثلث متساوی الاضلاع مرکز تقارن ندارد.
محور تقارن-
تعریف:
هر گاه قرینه هر نقطه از شکل
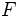
نسبت به خط ثابت
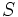
بر روی خود شکل قرار گیرد خط
را محور تقارن شکل گوییم. یک شکل ممکن است چندین محور تقارن داشته باشد.
خاصیت چهارم. بنا به نتیجه (1)و تعریف بالا هر گاه شکلی دارای دو محور تقارن عمود بر هم باشد، دارای مرکزتقارن است و محل تلاقی دو محور تقارن خواهد بود. مانند بیضی، دایره، مربع و …
خاصیت پنجم:
هر  ضلعی منتظم دارای
ضلعی منتظم دارای محور تقارن است. اگر
محور تقارن است. اگر  فرد باشد این محورهای تقارن از یک راس و وسط یک ضلع می گذرند مانند مثلث متساوی الاضلاع، پنج ضلعی منتظم و … و اگر
فرد باشد این محورهای تقارن از یک راس و وسط یک ضلع می گذرند مانند مثلث متساوی الاضلاع، پنج ضلعی منتظم و … و اگر زوج باشد نصف محورهای تقارن از وسط های اضلاع و نصف دیگر از راس ها می گذرند مانند مربع، شش ضلعی منتظم و … هم چنین دایره بی شمار محور تقارن دارد.
زوج باشد نصف محورهای تقارن از وسط های اضلاع و نصف دیگر از راس ها می گذرند مانند مربع، شش ضلعی منتظم و … هم چنین دایره بی شمار محور تقارن دارد.
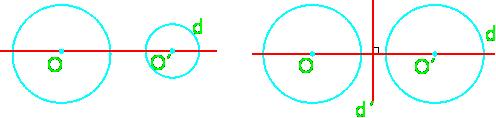
دو دایره با شعاع های مساوی و مرکز های متمایز دارای دو محور تقارن عمود بر هم می باشد و دو دایره با شعاع های نامساوی و مرکز های متمایز دارای یک محور تقارن می باشند که این محور تقارن امتداد خط المرکزین آن هااست و مماس مشترک های دو دایره نسبت به آن قرینه اند. هم چنین دو دایره متحد المرکز دارای بیشمار محورتقارن هستند.
 |
(الف) | (ب) |
هر خط راست بی شمار محور تقارن دارد
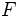 نسبت به خط ثابت
نسبت به خط ثابت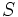 بر روی خود شکل قرار گیرد خط
بر روی خود شکل قرار گیرد خط 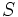 را محور تقارن شکل گوییم. یک شکل ممکن است چندین محور تقارن داشته باشد.
را محور تقارن شکل گوییم. یک شکل ممکن است چندین محور تقارن داشته باشد. ضلعی منتظم دارای
ضلعی منتظم دارای محور تقارن است. اگر
محور تقارن است. اگر  فرد باشد این محورهای تقارن از یک راس و وسط یک ضلع می گذرند مانند مثلث متساوی الاضلاع، پنج ضلعی منتظم و … و اگر
فرد باشد این محورهای تقارن از یک راس و وسط یک ضلع می گذرند مانند مثلث متساوی الاضلاع، پنج ضلعی منتظم و … و اگر زوج باشد نصف محورهای تقارن از وسط های اضلاع و نصف دیگر از راس ها می گذرند مانند مربع، شش ضلعی منتظم و … هم چنین دایره بی شمار محور تقارن دارد.
زوج باشد نصف محورهای تقارن از وسط های اضلاع و نصف دیگر از راس ها می گذرند مانند مربع، شش ضلعی منتظم و … هم چنین دایره بی شمار محور تقارن دارد.

