هلال بقراط
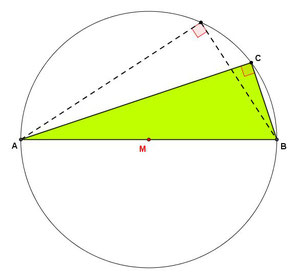
A، B و Cنقاطی روی دایره هستند.
اگرپاره خط AB قطر دایره باشد،
پس زاویه C همیشه زاویه راست=90 درجه.
2.)
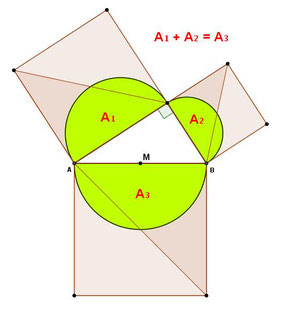
ثانیا طبق تئوری فیثاغورث:
مجذور وتر= مجذور یکصلع قائم + مجذور ضلع قائم دیگریا
مساحت مریع روی وتر= محت مربع روی یک ضلع قائم+ مساحت مربع روی ضلع قائم دیگر
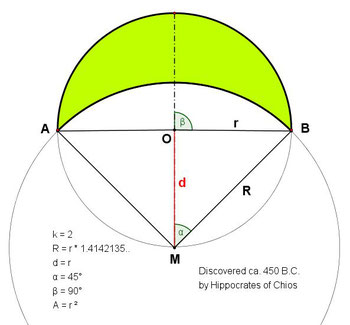
3.) شکل دیگ داریم به هلال بقراط معروف است.،
منظور بقراط پزشک نیست او در 450 بیش از میلاد می زیست.
به هلال ال هازن یا ابن هیثم هم معروف بود
ریاضی دان و منجم مسلمان مبتکر نورشناسی بین قرن 10و11 میلادی
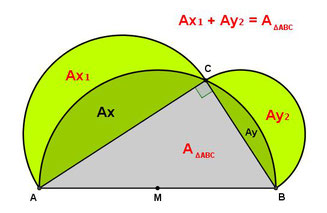
اگر مثلث قائم الزاویه ای داشته باشیم
بزرگترین نیم دایره وتر را می پوشاند،
دومقطع دایره ظاهر شده روی دوضلع دیگ مثلث قائم الزاویه (Axو Ay)که دولبه دونیمدایره قراردارند.
ودوقطعه نیم دایره (Ax1و Ay2)، را جدا کرده است و دوهلال(Ax1و Ay2)را ایجاد کرده است.
مساحت دوهلال (Ax1و Ay2)= مساحت مثلث قائم الزاویه ABC.
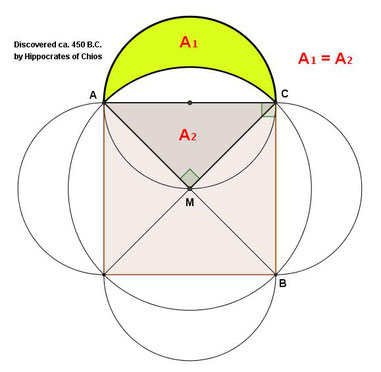
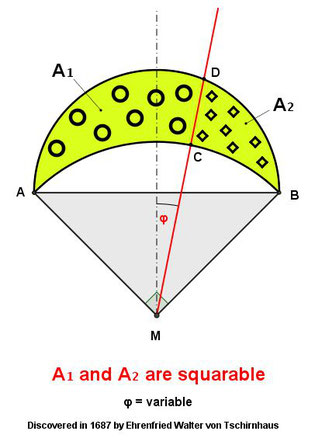
4.) در شکل بعدی شما یک قضیه جالب را می بینید:
اگر مثلث قائم الزاویه ABCیک مثلث قائم الزاویه متساوی الساقین باشد،
مساحت هلال A1=نصف مساحت مثلثABC که یعنی= مساحت AMC
نتیجه مساحت این هلال = ربع مساحت مربع
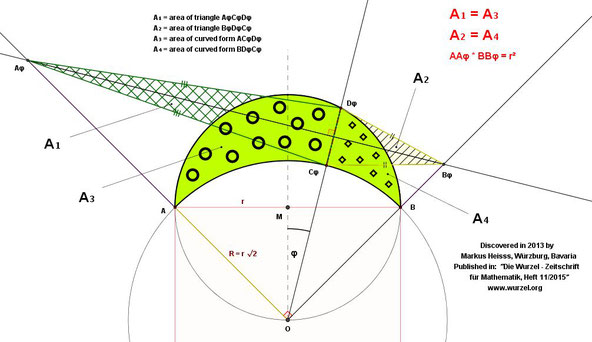
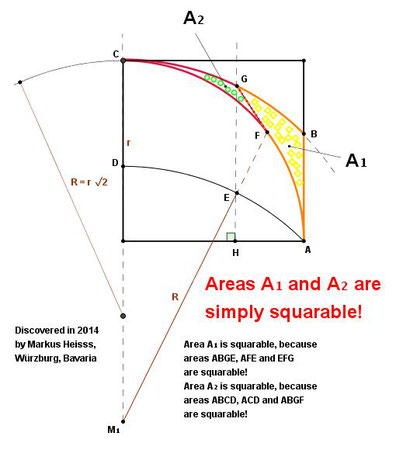
5.) درسال 1687 کشف شد که اگر خطی از مرکز Mرسم کنید و هلال روی یک ضلع مربع را به دوقسمت نامساوی تقسیم کنید باز
= همان ربع مساحت مربع:
.مارکوس هیس درسال2013 به قضایای دیگری رسید.
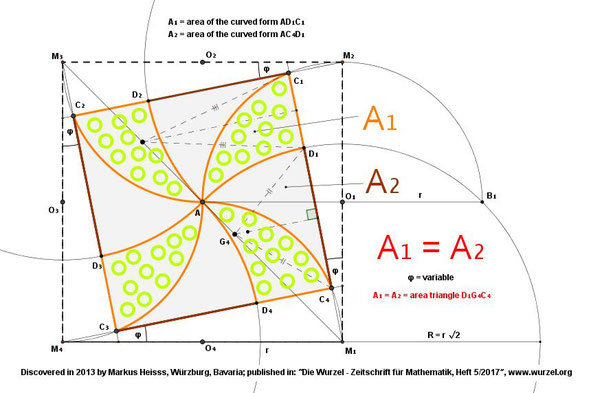
6.
7.) همچنین مدل چرخ بال که به نتایج جالبی دست یافت که مشاهده می کنید
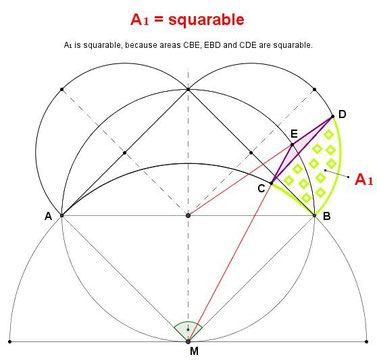
8.)
10)Just for completeness:
Nikolai Chebotaryov و Anatoly Dorodnov درسال 1947،
اعلام شد که با 5 هلال می توان به نتلیج جالبی دست یافت
که 3 هلال ان توسط بقراط اعلام شد و دوتای دیگر
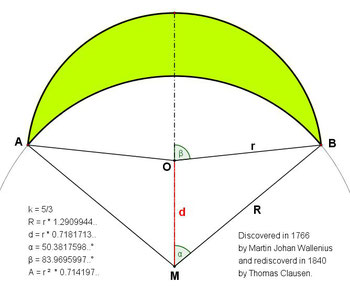
درسال1766 مارتین جان والنیوس.




1

- لینک منبع
تاریخ: شنبه , 13 آبان 1396 (23:21)
- گزارش تخلف مطلب