حدس گلد باخ

این مسئله در حدود 260 سال پیش توسط یک پزشک آلمانی علاقه مند به اثبات قضیه‌های ریاضی مطرح شد. شهود این پزشک متوجه حقیقت جالبی شده بود و آن هم این بود که هر عدد زوج را می‌توان به صورت مجموع دو عدد اول نوشت. (البته عدد یک را به این خاطر از مجموعه اعداد اول کنار گذاشتند که صورت مسئله‌های نظریه اعداد کوتاه تر شود. زیرا اگر این کار را نمی‌کردند بایستی در اکثر صورت مسئله‌های مربوط به اعداد اول می‌نوشتند: «به غیر از یک») اکنون به دلیل همین موضوع عدد 2 از حدس گلدباخ خارج شده‌است. گلدباخ هم عصر با اویلر بود. پس از تلاش فراوان و نا امید شدن از اثبات این حدس، گلدباخ از اویلر خواست تا مسئله را برایش حل کند. اویلر یکی از برجسته ترین شخصیت‌های ریاضی آن زمان بود. نه اویلر و نه هیچیک از شاگردانش نتوانستند این مسئله را حل کنند. تا اینکه حدود 6 سال پیش یک موسسه انتشاراتی در انگلستان به نام «تونی سیبر» برای کسی که بتواند این مسئله را حل کند مبلغ یک میلیون دلار جایزه تعیین کرد. این مسئله در عین سادگی صورت آن، هنوز حل نشده تا بتواند به عنوان قضیه مطرح شود.

این حدس توسط کامپیوترهای پیشرفته برای اعداد زوج بسیار بسیار بزرگی تست شده و جالب اینست که تا کنون هیچ مثال نقضی برای آن یافت نشده‌است.

گاهی اوقات فاصله شهود انسان تا لحظه اثبات یک مسئله آنقدر زیاد می‌شود که نسلها می‌آیند و می‌روند ولی همچنان حقیقت درباره مسئله‌ای مانند حدس گلد باخ نامشخص می‌ماند.

شاید حل نشدن این مسئله به این خاطر باشد که با اعداد اول سر و کار دارد. زیرا خود مجموعه اعداد اول نیز ساختار جبری معینی ندارد.

در سال 1742 گلدباخ طی نامه‌ای به اویلر می‌نویسد: ” به نظر می‌رسد که هر دو عدد زوج بزرگ‌تر از 2 را بتوان به صورت مجموع دو عدد اول نوشت.” این ادعای گلدباخ به حدس گلدباخ شهرت یافت و در این دو نیم قرن اخیر پایه و موضوع تحقیقات گسترده‌ای شده‌است.هاردی ریاضیدان برجسته انگلیسی تصریح می‌کند که حدس گلدباخ یکی از دشوارترین مسائل حل نشده ریاضیات است.

حدس گلدباخ: هر عدد صحیح زوج بزرگ‌تر از 2 را می‌توان به صورت مجموع دو عدد اول نوشت.

محاسبات عددی درستی این حدس را نشان می‌دهند که به طرق متعددی می‌توان اعداد زوج را به صورت مجموع دو عدد اول نوشت. در سال 1973 چن نشان داد که اعداد زوج به اندازه کافی بزرگ را می‌توان به صورت p+m نوشت که در آن p عددی اول و m عددی اول یا حاصل ضرب دو عدد اول است. گلدباخ حدس ضعیفتری زد که هر عدد فرد بزرگ‌تر از 7 را می‌توان به صورت مجموع سه عدد اول نوشت.هر چند که این مساله هنوز باز است اما وینوگراف در سال 1937 نشان داد که برای همه اعداد فرد مثبت به اندازه کافی بزرگ این قضیه درست است ولی اندازه کافی را تعریف نکرد. شاگرد آن برودزین اثبات کرد که عدد 3^14348907 به اندازه کافی بزرگ است (این عدد 6846169 رقم دارد!). در سال 2002 دو ریاضی دان این عدد را به حدود 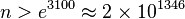کاهش دادند. یعنی اگر برای اعداد کوچکتر از آن درستی قضیه چک شود، اثبات کامل می‌شود ولی این کار از عهده کامپیوترهای فعلی برنمی آید.