مجموعه ها در ریاضی
مقدمه
تعریف مجموعه چیست؟ خوب، خیلی ساده، اجتماع، جمع آوری، گرد آوری
به تعدادی از اشیاء، اعداد، افراد، مشخص که گروهی را تشکیل بدهند و ازهم متمایز باشند مجموعه می گویند. هر یک از اشیاء، افراد، اعداد یک مجموعه یک عضو مجموعه نامیده می شوند.
حتی چیزهایی که عموما ویژگی مشترک دارند، را دریک گروه قرار می دهند هم یک مجموعه هستند.

مثال، پوشیدنی ها: کفش ها، جورابها،کلاه، پیراهن، شلوار، و.
شما می توانید تا 100تا یا بیشتر ادامه دهید.
علامت مجموعه { } است.
این یعنی مجموعه.
البته لازم نیست اعضای یک مجموعه ارتباط خاصی داشته باشند مثل:{خیام، 8، 5، تهران، اکبر}
مثال: دیگر انگشت های دست نشانه، میانی، انگشت حلقه، وکوچک. |  |
{.،91، 6، 3 }
هر یک از اعداد 3و6 و91 عضو مجموعه هستند.
{ } علامت مجموعه که عضوها را درون مجموعه می گذاریم وبین ها عضو کاما (،) می نویسیم.
. یعنی ادامه دارد.
نکات مهم دررابطه با مثال قبل:
چرا مثال اول در دنباله مجموعه 3 نقطه دارد؟ "." (3 نقطه).
این نقطه ها . جا افتاده ها یا حذف شده ها نام می گیرد که، منظور اینست که "ادامه دارد".
(یعنی اگر لیست را ادامه دهیم تا چندین مورد اضافه کنیم.،لیست ممکنست که تا یک ساعت یا بیشتر طول بکشد تا تمام شود شاید هم خیر بنابراین برای کوتاهی کار 3 نقطه می گذاریم.)
پس:
گروه اولی که 3 نقطه دارد {جورابها، کفشها، ساعت، پیراهن،.} یک مجموعه نامتناهی (تمام نشدنی) می گوییم،
دومین مجموعه {نشانه، میانی، انگشت حلقه، کوچک} را مجموعه متناهی (محدود-تمام شدنی) می گوییم.
گاهی "." دربین مجموعه نوشته شود:
مثال: لیست حروف انگلیسی:
{a، b، c،.، x، y، z}
این لیست متناهی نام دارد: (زیرا 26 حرف هست برای خلاصه نویسی کار چند حرف اول وچند حرف آخر را مینویسن وبین آنها. می گذارند?)
برای برخی از مجموعههای خاص، اسامی خاصی به کار میبریم که باید آنها را به خاطر سپرد:
- مجموعه اعداد طبیعی را با (N) نشان میدهیم و داریم.N{1،2،3،.}=N=
- مجموعه اعداد طبیعی نابیشتر از عدد طبیعی k را قطعهای از اعداد طبیعی میگوییم و به صورت نشان میدهیم و داریم
- N{1،2،3،.،K}=N=
- مجموعه همه اعداد اول را با P نشان میدهیم.
- مجموعه اعداد حسابی را با W نشان میدهیم و داریم.P{0،1،2،3،.،}=N=
- مجموعه اعداد صحیح را با Z={.،-2،-1،0،1،2،3،.،}=N نشان میدهیم.
مجموعه های عددی و شمارشی
در مبحث ریاضی ما مجموعه های زیادی داریم? می توانیم مجموعه هایی درریاضی می نویسیم که ویژگی مشترک داشته باشند، آیا می توان چنین مواردی را پیداکرد؟ بله:
و لیست مجموعه ها ادامه دارد. ما می توانیم مجموعه های بسیاری در ریاضی بنویسیم.
مجموعه هایی می نویسیم که هیچ وجه اشتراکی ندارند ولی یک مجموعه هستند. مجموعه زیر را با کمک کیبورد کامپیوتر تصادفی عددها را نوشتم ویک مجموعه ساختم. برای مثال:
چرا مجموعه ها اهمیت دارند؟
مجموعه ها یکی از مفاهیم بنیادی در ریاضی هستند.
یک گله گرگ، یک خوشه انگور یا یک دسته کبوتر، مثالهایی هستند از مجموعهها یی از اشیا. از این مفهوم ریاضی مجموعه، میتوان به عنوان اساسی برای تمامی ریاضیات امروزی استفاده کرد.
وقتی شما با مجموعه ها اشنا باشید ودرک بهتری از ریاضی پیدا می کنید. تئوری نموداری، انتگرال، اعدادحقیقی، اعدادمرکب، جبر خطی، تئوری اعداد، همه انها دریک چیز مشترکند: مجموعه.
مجموعه اصلی
 | مجموعه اصلی (مرجع یا عام)، مجموعه مادر،که مجموعه جهانی هم می گوییم. در هر بحث خاص مجموعه همه عناصر مورد بحث را عضو یک مجموعه کلی میگیریم و به آن مجموعه جهانی(Universal set) یا مرجع(عام) میگوییم. | |
 | مجموعه ها شامل: مجموعه عددهای صحیح، شامل کلیه عددهای مثبت و عددهای منفی و صفر مجموعه عددهای طبیعی: به عددهای صحیح مثبت عددهای طبیعی هم می گوییم. که مجموعه عددهای طبیعی زیر مجموعه عددهای صحیح هستند. Bزیر مجموعه A، گوییم. وقتی هر عضوB در عضوA هم هست. نماد  ، علامت زیرمجموعه بودن است. به عنوان مثال مینویسیم ، علامت زیرمجموعه بودن است. به عنوان مثال مینویسیم  | |
 | مجموعه عددهای حقیقی همه ی اعداد گویا و اصم مجموعه ای را تشکیل می دهند که به آن مجموعه اعداد حقیقی می گویند و با R نشان می دهند. |
نکات بیشتر:
 | عضویت برای مثال، A نام یک مجموعه هست، و a یک عضو این مجموعه A است. و مجموعه Bنام یک مجموعه است و b یک عضو مجموعه است، و C نام یک مجموعه هست و c عضو. |
مثال: مجموعه A داریم: {1،2،3}. ما می بینیم که m: 1![]() A
A
،اما n: 5 ![]() A عدد 5 عضو مجموعه A نیست.
A عدد 5 عضو مجموعه A نیست.
تساوی مجموعه ها
دو مجموعه زمانی با هم مساوی هستند که هر عضو A عضوB و هر عضو B عضو A باشد.
مثال: A و B دو مجموعه مساوی هستند:
مجموعه A شامل عددهای مثبت 1تا4
B = {4، 2، 1، 3}
بررسی کنیم. هر دو عدد 1 دارند، هر دو عدد 2 دارند. و 3، و 4. و تعداد اعضا هر مجموعه را می شماریم، 4 عضو بنابراین: بله، آنها مساویند!
علمت تساوی (=) را بین نام هر دو مجموعه می گذاریم: A = B
{1،2،8} نامساوی {1،2}
اگر دو مجموعه، زیر مجموعه یکدیگر باشند، آنگاه با یکدیگر مساوی خواهند بود.
زیر مجموعه 
ما مجموعه {1، 2، 3، 4، 5}A. را داریم زیر مجموعه ها ی این مجموعه {1، 2، 3} B که و {5، 4}و {1} و.
مثلا {1، 6} زیر مجموعه A نیست. زیرا 6 عضو آن نیست.
B زیر مجموعهA گوییم هرگاه هرعضو B عضوA نیز باشد.
B A
A
مثال: دیگر بزنیم: آیا A زیر مجموعه B چیست؟ { A = {1، 3، 4 و { B = {1، 4، 3، 2?
ببینید در مجموعه
در مجموعه A } A،و 1 و 3 و 4 هست در مجموعه B هم 1 و 4 و 3 هست.
پس A زیر مجموعه B که شامل عضوهایی که در A هست در B هم هست.
مثال: مجموعه A از مضربهای 4 و مجموعه B از مضربهای 2 تشکیل شده آیا A می تواند زیر مجموعه B باشد؟
B زیرمجموعه Aچطور
{.، 8،4،0،4-،8-،.} A
{.، 8، 6، 4،2،0،2-،4-، 6-، 8-،.} A
البته دو مجموعه نامتناهی هستند. بهتر است مقایسه ای انجام دهیم:
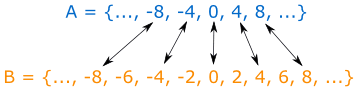
هر عضو A، عضو B هم هست. پس A می تواند زیر مجموعه B باشد. اما B نمی تواند زیر مجموعه A باشد. زیرا همه عضو های B در A نیست!
پس عبارت « .A زیر مجموعه B باشد
.A زیر مجموعه B باشد
نکته 1: اگر« » و «
» و « »، یعنی اگر هر عضو A در B وهر عضو B در A باشد، آنگاه A و B برابر خواهد بود یعنی A=B.
»، یعنی اگر هر عضو A در B وهر عضو B در A باشد، آنگاه A و B برابر خواهد بود یعنی A=B.
در ریاضیات معمولا برای آنکه نشان دهند دو مجموعه با هم برابرند، نشان می دهند که هرکدام زیر مجموعه ی دیگری است.
مثال:
{1، 2، 3} زیر مجموعه {1، 2، 3}، زیرا هر مجموعه زیر مجموعه خودش هم هست{1، 2، 3}.
مثال:
{1، 2، 3} یک زیر مجموعه {1، 2، 3، 4} است هرعضو اولی در مجموعه دومی هم هست.
اگر {1،2،8} B {1،2} A در این صورت B زیر مجموعه A است.
e: B ![]() A.
A.
A ![]() B ("معادل با این مطلب است که عضوی در A هست که متعلق به B نمیباشد")
B ("معادل با این مطلب است که عضوی در A هست که متعلق به B نمیباشد")
، A ![]() B.
B.
مجموعه تهی

مثال، مجموعه کلیدهای پیانو که روی گیتار است.
"صبرکنید!" شما می گویید، هیچ کلیدی روی گیتار نیست!"
درست گفتید. هیچی کلیدی روی گیتار نیست.
پس یک مجموعه خالی وتهی است. البته: صفر نه.
نماد مجموعه تهی ![]()
یا {} (مجموعه تهی هیچ عضوی ندارد)
مثال: مجموعه کشورهای جنوب قطب جنوب یک مجموعه تهی است.
مجموعه تهی، زیرمجموعه تمام مجموعه ها است.
تنها زیرمجموعه مجموعه تهی، خودش است.
تعداد اعضای مجموعه تهی صفر است و به عبارتی متناهی است:
اگر هر عضو مجموعه تهی در مجموعه A باشد پس مجموعه تهی مساوی مجموعهA زیرا عضوی ندارد.
- لینک منبع
تاریخ: جمعه , 27 مهر 1397 (19:49)
- گزارش تخلف مطلب
