رابطه جالب در دنباله اعداد فیبوناتچی

دنباله ی فیبوناتچی، دنباله ای از اعداد است که جمله اول و دوم آن برابر یک می باشد و جملات دیگر آن از جمع دو جمله قبلی در این دنباله به دست می آید: 

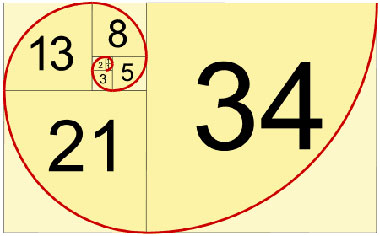
...,1,1,2,3,5,8,13,21,34,55 

این دنباله، یک دنباله شگفت انگیز و بسیار جالب در ریاضی است و در بسیاری از پدیده ها در طبیعت مثل تولید مثل خرگوش ها?،رشد گیاهان☘️ و... نمود پیدا می کند.

هم چنین اگر هر جمله این دنباله را به جمله قبل از خودش در این دنباله تقسیم کنیم و این کار را همین طور ادامه دهیم، به عدد طلایی? (1/68) نزدیک می شویم. 

در این دنباله، رابطه جالب دیگری نیز وجود دارد. به این صورت که اگر a,b,c به ترتیب، اعدادی باشند که در این دنباله قرار دارند، رابطه ی زیر برقرار است:  

 1 (به اضافه یا منهای)  +_ b مجذور = ac

برای مثال عدد های 1,1,2 در این دنباله را در نظر بگیرید:

1 + 1 به توان دو = 1×2

یا اعداد 1,2,3 در این دنباله: 

1 _ 2 به توان دو = 1×3

اعداد 2,3,5:  

1 + 3 به توان دو = 2×5

اعداد 3,5,8: 

1 _ 5 به توان دو = 3×8

و به همین ترتیب، این رابطه در هر سه عدد متوالی در دنباله فیبوناتچی برقرار است.

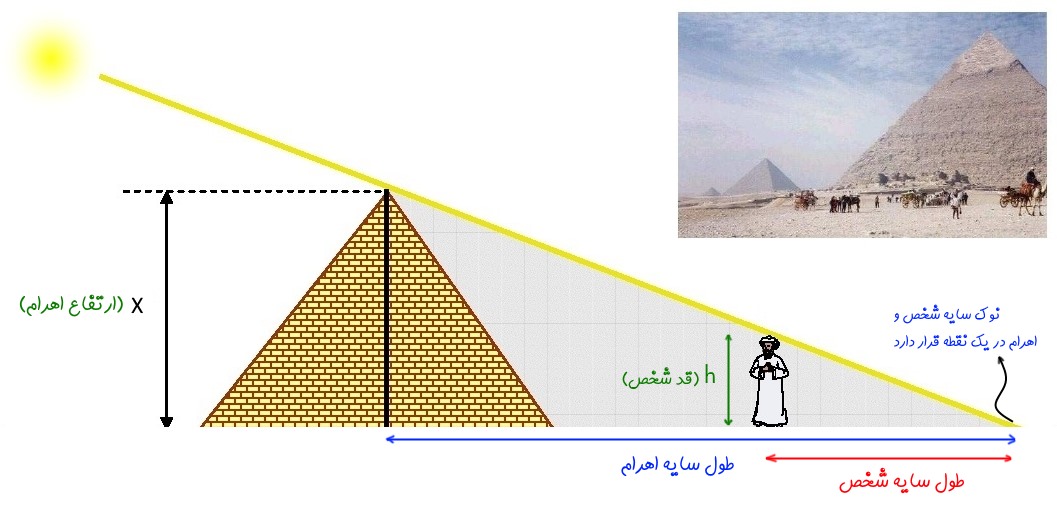آیا می توان بدون اندازه گیری مستقیم، طول یک شی بلند مثلا ارتفاع یک درخت یا ساختمان ده طبقه را اندازه گیری کرد؟!

تالس، یک دانشمند یونانی بوده که اسم او را در کتاب های علوم و یا شیمی هم شاید دیده باشید. (تالس، آب را تنها عنصر اصلی سازنده جهان می دانست)

شاید فکر کنید که تالس، اولین کسی بود که قضیه ی تالس را کشف کرد و آن را به نام خود کرد، اما این گونه نیست. پیش از تالس، مصریان نیز با قضیه تالس آشنایی داشتند و از آن برای ساخت بناها و اهرام استفاده می کردند، اما اثباتی برای آن نداشتند. در واقع تالس، نخستین کسی بود که درستی قضیه ی تالس را اثبات کرد و به همین دلیل، این قضیه به نام او نام گذاری شد.

تالس توانست با استفاده از قضیه ی تالس، ارتفاع اهرام ثلاثه مصر را اندازه گیری کند. هم چنین وقتی او از مصر با کشتی برمی گشت، توانست فاصله ی کشتی تا ساحل را اندازه گیری کند.

ما با استفاده از قضیه ی تالس می توانیم، ارتفاع هر شی بلندی را اندازه گیری کنیم. اشیایی که اندازه گیری طول و ارتفاع آن ها به صورت مستقیم، دشوار و سخت است. در حقیقت، ما با استفاده از یک خط کش (یا یک شخص) و طول سایه ی آن و هم چنین طول سایه ی شی بلند می توانیم طول شی را اندازه بگیریم.

قضیه تالس: هر چند خط موازی، دو خط مورب را قطع کنند، بر روی خطوط مورب پاره خط هوایی ایجاد می شود که با طول این پاره خط ها با هم متناسب است.

تعمیم قضیه تالس: هر گاه خطی موازی با یکی از اضلاع مثلث رسم شود، دو ضلع دیگر مثلث را قطع می کند و بر روی آن دو ضلع، پاره خط هوایی ایجاد می کند که طول این پاره خط ها با هم متناسب است.

عدد چهار را در نظر بگیرید (4). حال اگر کنار این عدد، علامت تعجب قرار دهیم، دیگر مفهوم آن، عدد چهار نیست (!4). 

در ریاضی، وقتی علامت تعجب رو به روی یک عدد قرار می گیرد، مفهومش این است که حاصل آن از حاصل ضرب آن عدد در همه ی اعداد قبل از خودش تا یک (یا به عبارتی اعداد کوچکتر از خودش تا یک) به دست می آید. یعنی: 

1×2×3×4=!4

در واقع، همه ی این اعداد قبلی یا عوامل قبلی دست به دست هم داده اند، تا عدد!4 به دست آید.

هر یک از ما انسان ها نیز در زندگی به نوعی عددی برحسب فاکتوریل هستیم. چرا که عواملی از جمله خانواده، پدر و مادر، معلمان و اساتید، دوستان و...  و از همه مهم تر خدای بزرگ، دست به دست هم داده اند تا ما به موفقیت و جایگاهی که الان داریم، برسیم.

پس بیایم همیشه قدرشناس فاکتوریل های زندگیمون باشیم.?

راستی فاکتوریل های زندگی شما چه کسانی هستند؟ 

(برگرفته شده از پیج اینستاگرامی ریاضی دو دو تا)