آرایه مراعات نظیر یا تناسب
- ادامه مطلب
تاریخ: شنبه , 06 اسفند 1401 (18:13)
- گزارش تخلف مطلب
تاریخ: شنبه , 06 اسفند 1401 (18:13)
تاریخ: شنبه , 06 اسفند 1401 (08:13)
در این قسمت میخواهیم یک عدد گویا(اعشاری) را به مبنای دلخواهی ببریم.
 به عنوان مثال میخواهیم عدد 8/56 قسمت قبلی را به مبنای 5 برگردانیم.برای اینکار:
به عنوان مثال میخواهیم عدد 8/56 قسمت قبلی را به مبنای 5 برگردانیم.برای اینکار:
::.ابتدا جزء صحیح را همانند اعداد طبیعی به مبنای مورد نظر میبریم
(8)10=(13)5
تذکر: برای قسمت اعشاری کافیست آن را در مبنا ضرب کنیم.بعد از ضرب، رقمی که به پشت ممیز(جزء صحیح) منتقل می شود اولین رقم مبنا بعد از ممیز را تشکیل می دهد a
بار دیگر جزء اعشاری حاصل را در مبنا ضرب می کنیم و رقمی که در حاصلضرب به جزء صحیح منتقل می شود را به عنوان دومین رقم مبنا بعد از ممیز انتخاب می کنیم((b.و این عمل را همچنان ادامه میدهیم تا بقیه ارقام مبنا بدست آید.در مثال ما همانطور که می بینید بعد از دو مرحله جزء اعشاری به صفر رسیده.
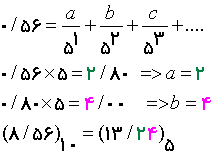
تذکر: ممکن است دو حالت پیش بیاید یا قسمت اعشاری به صفر برسد که در اینصورت کار تمام است. و یا ممکن است قسمت های اعشاری دوباره تکرار شوند که در اینحالت دوره گردش به وجود میاید.
عدد12/25 را به مبنای 3 ببرید. ابتدا 12 را به مبنای 3 میبریم که مقدار آن (110)3 خواهد شد.حالا جزء اعشاری را حساب می کنیم.
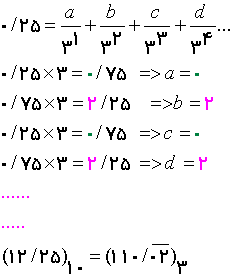
همانطور که در شکل بالا می بینید ارقام صفر و دو تکرار می شوند.
در خاتمه امیدوارم این مطالب مورد استفاده شما قرار گرفته باشد!مطمئناً این نوشته ها کامل نیست و خوشحال می شوم اگر چنانچه نکته ای از قلم افتاده،شما دوست محترم آنرا در این قسمت برای اطلاع بنده و دیگر عزیزان بازگو کنید.
تاریخ: پنجشنبه , 04 اسفند 1401 (04:47)
قاعده های بخش پذیری بر اعداد
یکی از موضوعاتی که دانش آموزان در ریاضیات ودر پایه های مختلف به آن نیاز دارند قاعده ها بخش پذیری بر اعداد است. باید سعی شود این قاعده ها را خود دانش آموزان به دست آورندو از آن استفاده کنند. در زیر قاعده های بخش پذیری بر 1 تا 15 بیان شده است.
قاعده تقسیم بر 1:
همه ی اعداد بر یک بخش پذیر هستند.
قاعده تقسیم بر 2:
عددی بر 2 بخش پذیر است که رقم یکانش زوج باشد.
مثال- 1354 بر 2 بخشپذیر است.
قاعده تقسیم بر 3:
عددی بر 3 بخش پذیر است که مجموع ارقامش بر 3 بخش پذیر باشد. مثال- مجموع رقم های عدد 2346 برابر 15 است و 15 بر 3 بخش پذیر می باشد، بنابراین عدد2346بر 3 بخش پذیر است.
قاعده تقسیم بر 4:
الف) عددی بر 4 قابل قسمت است که دو رقم سمت راست آن بر4 قابل قسمت باشد.
مثال- عدد 9148 بر 4 بخش پذیر است. زیرا 48 بر 4 بخش پذیر است.
ب) عددی بر4 بخش پذیر است که رقم یکان به اضافه ی 2 برابر رقم دهگان آن بر 4 بخش پذیر باشد.
مثال- عدد 1568 بر 4 بخش پذیر است. زیرا + 6×2 و 20 بر 4 بخش پذیر می باشد.
تاریخ: پنجشنبه , 04 اسفند 1401 (03:47)
انواع اشتباهات را می توان در جدول مقابل مشاهده کرد.
|
غلط |
درست |
نوع اشتباه |
|
سبح |
صبح |
حافظه دیداری |
|
بشکاب |
بشقاب |
حساسیت شنیداری |
|
می گوفت |
می گفت |
آموزش |
|
داسبتان |
داستان |
دقت |
|
به صورت وارون |
بابا |
وارونه نویسی |
|
به صورت قرینه -از چب به راست |
بابا |
قرینه نویسی |
|
مارد |
مادر |
حافظه توالی دیداری |
|
امیر الموءمنین (به صورت کج) |
امیرالموءمنین |
نارسا نویسی |
|
جانه |
خانه |
تمیز دیداری – دقت |
حساسیت شنیداری:
همان چیزی را که تلفظ می کند بنویسید
اضافه کردن به انتهای فعل و درست ننوشتن شناسه
حذف حروف(نوشتن صب به جای صبح)
آموزشی:
به هم پیوسته نوشتن کلمات جدا از هم
اضافه کردن ه به کلمات (مثل بنده گان به جای بندگان)
اشتباه نوشتن ُ به جای او- و و بالعکس
اشتباه نوشتن حروف والی (مثل نوشتن امیرلمومنین به جای امیرالمومنین)
نوشتن ه به جای ِ و بالعکس(مثل: دیدنه پدر به جای دیدنِِ پدر)
دقت:
کم یا زیاد گذاشتن نقطه یا دندانه یا سرکج
اضافه گذاشتن حروف در کلمه(مثل سینمبا به جای سینما)
کم گذاشتن حروف در کلمه(مثل سرده به جای سپرده)
حافظه دیداری: استفاده از حروف هم صدا به جای هم
حافظه شنیداری: جا انداختن کلمات
حافظه توالی شنیداری: جا به جا نوشتن حروف یا کلمه
قرینه نویسی: از چپ به راست نوشتن(آیینه نویسی)
وارونه نویسی: برعکس نوشتن
بدخطی
تمارین تقویت حافظه دیداری:
تمرین 1- نشان دادن تصویر و مخفی کردن آن(شروع از 2 تصویر)- کارت دید آموز
تمرین 2- نشان دادن یک تصویر مرکب و پرسش از جزئیات آن(پس از مخفی کردن)
تمرین 3 - مخفی یا جا به جا کردن یکی از وسایل روی میز و حدس زدن آن
تمرین 4- دادن کارت کلمات به فراگیر و انجام تمارین 1 و 3 با کارت کلمات
تمرین 5- استفاده از روش فرنالد
تاریخ: پنجشنبه , 04 اسفند 1401 (02:47)
زاویه بین ساعت شمار و دقیقه شمار
برای این که زاویه بین عقربه ساعت شمار و دقیقه شمار در زمان معین را بدست آوریم باید ساعت را در 30 و دقیقه را در 5.5 ضرب کنیم و حاصل این دو را از هم کم کنیم.
علت این کار چیست؟
در فاصله ی بین دو ساعت، عقربه ساعت شمار، 30 درجه از دایره را طی می کند.
و در فاصله ی بین دو دقیقه هم عقربه دقیقه شمار 6 درجه می پیماید اما در همین زمان، ساعت شمار به اندازه 0.5 درجه جلو می رود و در نتیجه دقیقه شمار به اندازه ی 5.5 درجه با آن اختلاف خواهد داشت.
اگر زاویه به دست آمده از 180 درجه بیشتر شود، آن را از 360 کم می کنیم.
مثال: در ساعت 3: '45 زاویه بین دو عقربه ساعت شمار و دقیقه شمار چند درجه است؟
3×30=90
45× 5.5=247.5
247.5-90=137.5
تاریخ: پنجشنبه , 04 اسفند 1401 (01:47)
عدد طلائی عددیست، تقریباَ مساوی 1.618، که خواص جالب بسیاری دارد،اشکال تعریف شده با نسبت طلائی، از نظر زیبائی شناسی در فرهنگهای غربی دلپذیر شناخته شده، چون بازتابنده خاصیتی بین تقارن و عدم تقارن است.
پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. اگر این معادله ساده یعنی a2=ab+b را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا
1.61803399 یا 1.618 خواهیم رسید.
تعریف دیگر نسبت طلایی این است که «عددی مثبت است که اگر به آن یک واحد اضافه کنیم به مربع آن خواهیم رسید». تعریف هندسی آن چنین است: طول مستطیلی به مساحت واحد که عرض آن یک واحد کمتر از طولش باشد.
بسیاری از مراجع علمی، حرف یونانی φ را برای این عدد انتخاب کردهاند.
. اگر عدد فی را بتوان دو برسانیم مثل این است که یک واحد به عدد فی افزوده باشیم یعنی Φ²=Φ+1 و اگر عدد یک را بر فی تقسیم کنیم مثل این است که یک واحد از عدد فی کم کرده باشیم یعنی:
1/Φ=Φ-1
پوسته مارپیچی یک حلزون نمونه ای ساده ودرعین حال زیبا، از نسبت طلائی است.
نسبت قطر مارپیچ های حلزون نیز نسبت 1.618 به یک را دارد.حلزون گوش
تاریخ: پنجشنبه , 04 اسفند 1401 (00:47)