حجم و مساحت
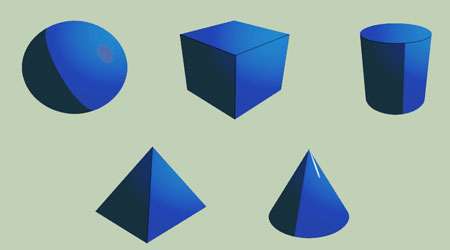
سطح
فرمول مساحت برخی اشکال هندسی دوبعدی به صورت زیر است:
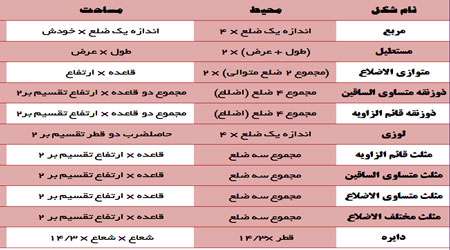
اما در مورد اشکال هندسی سه بعدی و دارای حجم برای بدست آوردن مساحت جانبی و مساحت کل هر شکل، می توان از رسم گسترده آن(یعنی باز کردن آن در فضای دو بعدی) بر روی صفحه و محاسبه مساحت هر یک از سطوح استفاده کرد.
مثال: با توجه به گسترده ی هر یک از حجم های زیر، مساحت گسترده را بدست آورید.
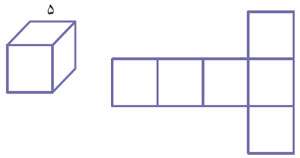
جواب: شش مربع داریم که مساحت هر کدام برابر است با 25=52 پس مساحت کل برابر است با150= 6*25.
حجم های حاصل از دوران شکل های هندسی
1- کره
تعریف دایره: مجموعه نقاطی از صفحه است که همه آن نقاط از یک نقطه در همان صفحه به نام مرکز به یک فاصله است. به این اندازه ثابت، شعاع می گویند.
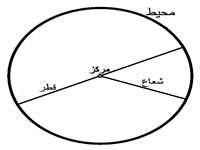
از دوران یک نیم دایره حول قطر آن، یک کره بوجود می آید.
کره، مجموعه نقاطی از فضاست که همه آن نقطه ها از یک نقطه به نام مرکز به یک فاصله ثابت و مشخص هستند. به این اندازه ثابت، شعاع کره می گویند
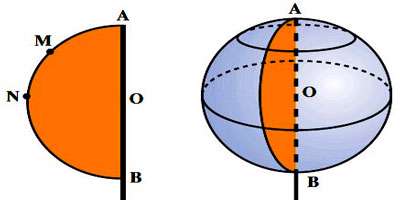
حجم و مساحت کره:
1-حجم کره ای با شعاع R از رابطه زیر بدست می آید:
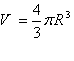
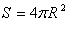
2- استوانه
از دوران مستطیل حول اضلاع آن، استوانه بدست می آید. در این صورت قاعده آن به شکل دایره خواهد شد. و شعاع دایره همان شعاع استوانه خواهد بود.
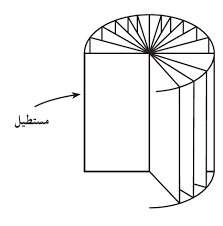
حجم استوانه: اگر شعاع استوانه r باشد و بلندی آن h، آنگاه حجم آن برابر خواهد بود با:
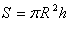
سطح کل استوانه = سطح دو قاعده + مساحت جانبی (مساحت مجموع دو قاعده + ارتفاع × پیرامون قاعده)
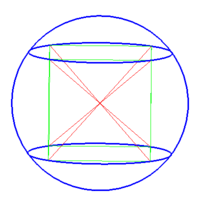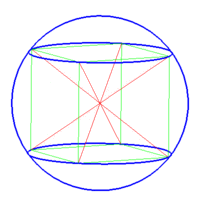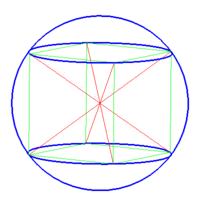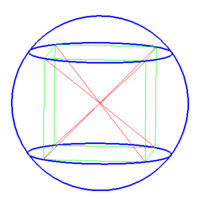
در شکل روبرو کره را طوری درون استوانه قرار داده ایم که کره کاملاً از بالا و پایین و اطراف بر استوانه مماس شده است.
در این حالت می گوییم کره در استوانه محاط شده است. استوانه نیز بر کره محیط شده است.
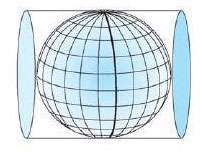
شعاع قاعده استوانه برابر R و ارتفاع آن برابر 2R است.
در نتیجه

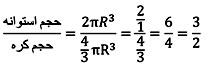
با استفاده از حجم کره و استوانه می توان گفت که حجم استوانه یک و نیم برابر حجم کره است.
3- مخروط
از دوران مثلث قائم الزاویه حول هر یک از اضلاع قائمه یک مخروط بدست می آید.
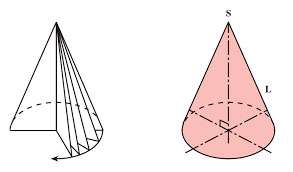
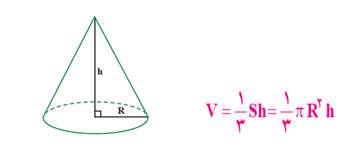
حجم مخروط: اگر شعاع قاعده مخروط r باشد و ارتفاع آن h، آنگاه حجم آن برابر خواهد بود با:
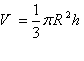
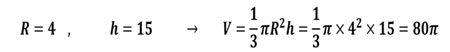
 تعریف هرم
تعریف هرم
هرم یک چندوجهی است که همه وجه های آن به جز یکی در یک راس مشترکند. ارتفاع هرم پاره خطی است که از راس هرم بر قاعده آن عمود میشود. وجهی از هرم که راس هرم در آن قرار ندارد قاعده و وجههای دیگر وجههای جانبی نامیده میشوند. وجههای جانبی همواره به شکل مثلث هستند. به هر یک از مثلث هایی که در یک نقطه همدیگر را قطع می کنند، وجه جانبی هرم می گویند.
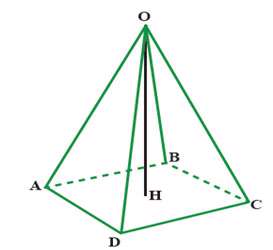
هرم منتظم: اگر چندضلعی قاعده یک چندضلعی منتظم بوده و وجه های جانبی با هم همنهشت باشند، هرم را منتظم می گویند.
حجم هرم
حجم هرم با مساحت S و ارتفاع h برابر است با:
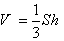
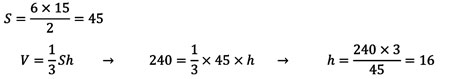
نکته:
مخروط شکلی شبیه هرم منتظم است که قاعده آن به شکل دایره و پای ارتفاع در مرکز دایره است.
- لینک منبع
تاریخ: سه شنبه , 29 بهمن 1398 (22:05)
- گزارش تخلف مطلب
