فرمول حجم استوانه در ریاضی با طعم پیتزا

Pizza = حجم یا همان V 

P : همان عدد پی π 

zz: مجذور شعاع 

a:  ارتفاع پیتزا 

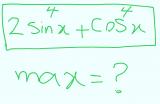
برای به دست آوردن مقدار ماکزیمم تابع مثلثاتی بالا، می دانیم که:

sin به توان دو + cos به توان دو = 1

یعنی ماکزیمم توان زوج های sin و cos، برابر یک است و اگر مقدار یکی از آن ها، یک باشد، مقدار دیگری حتما برابر صفر است.

از طرف دیگر می دانیم:

مقدار های sin  و cos همواره بین منفی یک تا مثبت یک است.

پس برای این که مقدار عبارت بالا، ماکزیمم شود، ابتدا دقت می کنیم که کدام یک ضریب بزرگتری دارد. چون sin به توان چهار، ضریب بزرگتری دارد، پس برای این که بیشترین مقدار ممکن تولید شود، باید مقدار sin، بیشترین مقدار خود یعنی یک باشد. از طرفی می دانیم اگر مقدار یکی از آن ها، برابر یک شد، مقدار دیگری حتما باید صفر باشد.

2 = ​​​​​​max = 2 + 0 

اگر دو عدد دو رقمی داشته باشیم که رقم یکان هر دو، عدد 1  باشد، در این صورت برای ضرب سریع تر این اعداد می توانیم از روشی که با نمونه گفته می شود، استفاده کنیم:

=41×21

ابتدا حاصل ضرب رقم های یکان در هم که برابر 1 می شود، را می نویسیم:

1=1×1

1  ---  ---  =41×21

سپس حاصل جمع رقم های دهگان را به دست آورده و می نویسیم:

6=2+4

1    6   ---   =41×21

حال حاصل ضرب ارقام دهگان را محاسبه کرده و می نویسیم: 

8=4×2

861=41×21

نکته: در صورتی که حاصل جمع ارقام دهگان، بیشتر از ده شود، در این صورت رقم یکان حاصل جمع را نوشته و رقم دهگان آن را نگه داشته و با حاصل ضرب ارقام دهگان که در مرحله بعد به دست می آوریم، جمع می کنیم.

اکنون به نمونه های ذکر شده در زیر دقت کنید:

=91×31

1=1×1

2  طبق نکته، رقم یکان آن را می نویسیم  12=9+3

28=1+ 27  27=3×9

2821=91×31

=51×41

1=1×1

9=5+4

20=5×4

2091=51×41

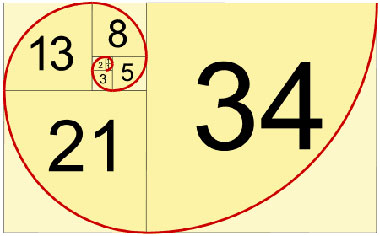دنباله ی فیبوناتچی، دنباله ای از اعداد است که جمله اول و دوم آن برابر یک می باشد و جملات دیگر آن از جمع دو جمله قبلی در این دنباله به دست می آید: 

...,1,1,2,3,5,8,13,21,34,55 

این دنباله، یک دنباله شگفت انگیز و بسیار جالب در ریاضی است و در بسیاری از پدیده ها در طبیعت مثل تولید مثل خرگوش ها?،رشد گیاهان☘️ و... نمود پیدا می کند.

هم چنین اگر هر جمله این دنباله را به جمله قبل از خودش در این دنباله تقسیم کنیم و این کار را همین طور ادامه دهیم، به عدد طلایی? (1/68) نزدیک می شویم. 

در این دنباله، رابطه جالب دیگری نیز وجود دارد. به این صورت که اگر a,b,c به ترتیب، اعدادی باشند که در این دنباله قرار دارند، رابطه ی زیر برقرار است:  

 1 (به اضافه یا منهای)  +_ b مجذور = ac

برای مثال عدد های 1,1,2 در این دنباله را در نظر بگیرید:

1 + 1 به توان دو = 1×2

یا اعداد 1,2,3 در این دنباله: 

1 _ 2 به توان دو = 1×3

اعداد 2,3,5:  

1 + 3 به توان دو = 2×5

اعداد 3,5,8: 

1 _ 5 به توان دو = 3×8

و به همین ترتیب، این رابطه در هر سه عدد متوالی در دنباله فیبوناتچی برقرار است.

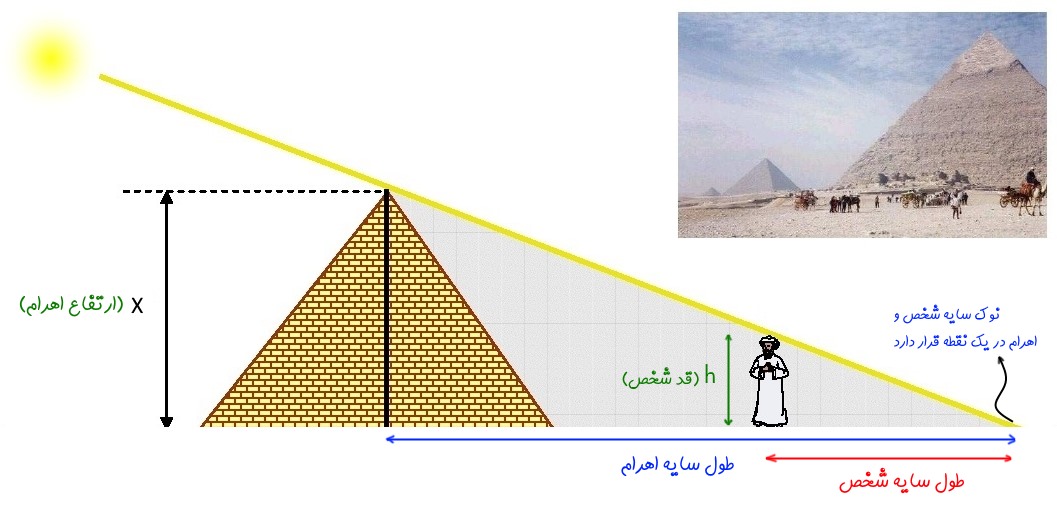آیا می توان بدون اندازه گیری مستقیم، طول یک شی بلند مثلا ارتفاع یک درخت یا ساختمان ده طبقه را اندازه گیری کرد؟!

تالس، یک دانشمند یونانی بوده که اسم او را در کتاب های علوم و یا شیمی هم شاید دیده باشید. (تالس، آب را تنها عنصر اصلی سازنده جهان می دانست)

شاید فکر کنید که تالس، اولین کسی بود که قضیه ی تالس را کشف کرد و آن را به نام خود کرد، اما این گونه نیست. پیش از تالس، مصریان نیز با قضیه تالس آشنایی داشتند و از آن برای ساخت بناها و اهرام استفاده می کردند، اما اثباتی برای آن نداشتند. در واقع تالس، نخستین کسی بود که درستی قضیه ی تالس را اثبات کرد و به همین دلیل، این قضیه به نام او نام گذاری شد.

تالس توانست با استفاده از قضیه ی تالس، ارتفاع اهرام ثلاثه مصر را اندازه گیری کند. هم چنین وقتی او از مصر با کشتی برمی گشت، توانست فاصله ی کشتی تا ساحل را اندازه گیری کند.

ما با استفاده از قضیه ی تالس می توانیم، ارتفاع هر شی بلندی را اندازه گیری کنیم. اشیایی که اندازه گیری طول و ارتفاع آن ها به صورت مستقیم، دشوار و سخت است. در حقیقت، ما با استفاده از یک خط کش (یا یک شخص) و طول سایه ی آن و هم چنین طول سایه ی شی بلند می توانیم طول شی را اندازه بگیریم.

قضیه تالس: هر چند خط موازی، دو خط مورب را قطع کنند، بر روی خطوط مورب پاره خط هوایی ایجاد می شود که با طول این پاره خط ها با هم متناسب است.

تعمیم قضیه تالس: هر گاه خطی موازی با یکی از اضلاع مثلث رسم شود، دو ضلع دیگر مثلث را قطع می کند و بر روی آن دو ضلع، پاره خط هوایی ایجاد می کند که طول این پاره خط ها با هم متناسب است.

عدد چهار را در نظر بگیرید (4). حال اگر کنار این عدد، علامت تعجب قرار دهیم، دیگر مفهوم آن، عدد چهار نیست (!4). 

در ریاضی، وقتی علامت تعجب رو به روی یک عدد قرار می گیرد، مفهومش این است که حاصل آن از حاصل ضرب آن عدد در همه ی اعداد قبل از خودش تا یک (یا به عبارتی اعداد کوچکتر از خودش تا یک) به دست می آید. یعنی: 

1×2×3×4=!4

در واقع، همه ی این اعداد قبلی یا عوامل قبلی دست به دست هم داده اند، تا عدد!4 به دست آید.

هر یک از ما انسان ها نیز در زندگی به نوعی عددی برحسب فاکتوریل هستیم. چرا که عواملی از جمله خانواده، پدر و مادر، معلمان و اساتید، دوستان و...  و از همه مهم تر خدای بزرگ، دست به دست هم داده اند تا ما به موفقیت و جایگاهی که الان داریم، برسیم.

پس بیایم همیشه قدرشناس فاکتوریل های زندگیمون باشیم.?

راستی فاکتوریل های زندگی شما چه کسانی هستند؟ 

(برگرفته شده از پیج اینستاگرامی ریاضی دو دو تا)

می دانیم عبارت جلوی یک لگاریتم باید همواره مثبت باشد، در واقع لگاریتم برای اعداد صفر و منفی تعریف نشده است.

اما جواب لگاریتم یک عبارت، مجموعه ی تمام اعداد حقیقی است. یعنی حاصل لگاریتم یک عبارت هم می تواند منفی باشد، هم مثبت و هم صفر (لگاریتم یک، برابر صفر است).

حال با توجه به این نکته که حاصل لگاریتم یک عدد، مثبت شود یا منفی، می توان به ماهیت آن عدد پی برد.

اگر حاصل لگاریتم یک عدد مثل x، مثبت باشد، در این صورت داریم: 

1 + [log x] = تعداد ارقام عدد x

حال اگر حاصل لگاریتم یک عدد مثل x، منفی باشد، در این صورت داریم:

1 + [log x] = تعداد صفرهای بعد از اعشار x

منظور از [ ]، جز صحیح یا براکت است.

متغیرهای کمی و کیفی:

متغیر کیفی: مقادیر عددی ندارند و جنبه توصیفی دارند و دو نوع هستند اسمی و ترتیبی.

متغیر اسمی، متغیر کیفی و توصیفی هست که ترتیب در آن وجود ندارد مثل گروه خونی (A,B,AB,O)، جنسیت (خانم و آقا).

متغیر ترتیبی، متغیر کیفی و توصیفی هست که ترتیب در آن وجود دارد مثل پایه های تحصیلی (اول، دوم، سوم و...)، میزان تحصیلات (دیپلم، لیسانس و...).

متغیر کمی: مقادیر عددی دارند که دو نوع هستند متغیر فاصله ای و نسبتی.

متغیر فاصله ای، متغیر عددی و کمی هست که صفر مطلق ندارد. مقادیر آن به نوعی قراردادی هستند. نسبت آن ها، بی معنا هست مثل درجه هوا و میزان هوش افراد.
اعداد مربوط به درجه هوا، مقادیر قرار دادی هستند، در واقع زمانی که آب، یخ می زند دمای آن را صفر و زمانی که می جوشد دمای آن را 100 در نظر گرفته اند و فاصله بین این صفر تا صد را به صد قسمت تقسیم کرده اند. نسبت دمای هوای دو شهر معنی ندارد و نمی توان گفت دمای هوای شهری، دو برابر دمای شهر دیگر هست.
برای سنجش هوش افراد نیز مقادیر عددی قراردادی هستند و صفر مطلق در آن معنا ندارد و نمی توان گفت هوش کسی صفر هست.

متغیر نسبتی، متغیر عددی و کمی هست که صفر مطلق دارد، مقادیر آن قراردادی نیست و نسبت آن ها با معنا هست مثل قد، وزن، تعداد افراد.
قد، وزن و تعداد افراد می تواند صفر مطلق باشد یعنی وجود نداشته باشد و می توان گفت قد، وزن، تعداد افراد دو برابر قد، وزن و تعداد افرادی دیگر هست، به عبارتی نسبت آن ها با معنا هست.

آزمون شیمی هفتم

هر دو این فرآیندها را می توان به سادگی به اعداد چند رقمی نیز گسترش داد.در بیشتر کتابهای درسی نیز برای کار با مقسوم علیه های چند رقمی دو فرآیند به کارگرفته می شود که حاوی یک عدد حدسی برای انتخاب مقسوم علیه است.هیچ یک از این روش ها جامعیت ندارند؛ ولی هر دوی آنها، یعنی روش ظاهری و روش گرد کردن به فراوانی تدریس می شوند.

روش ظاهری

تنها نخستین رقم مقسوم علیه به عنوان یک شکل امتحانی مورد استفاده قرار می گیرد:

چند تا 3 تایی در 8 وجود دارد ؟            876 تقسیم بر 34

چند تا 5 تایی در 47 وجود دارد؟           472 تقسیم بر 57

روش گرد کردن

وقتی رقم دوم از چپ در مقسوم علیه دو رقمی 4 یا کوچک تر از آن باشد، روش گرد کردن مانند همان روش ظاهری خواهد بود.وقتی که این رقم 5، 6، 7، 8 یا 9 باشد، به رقم دهگان یک واحد می افزاییم و سپس آن را به عنوان مقسوم علیه ظاهری به کار می گیریم.

چند تا 3 تایی در 8 وجود دارد؟     876 تقسیم بر 34

چند تا 6 تایی در 47 وجود دارد؟      472 تقسیم بر 57

چون 57 به 60 نزدیک تر از 50 است ،استفاده از 60 برآورد دقیق تری خواهد بود.

هریک از این روش ها به تصحیح نیاز دارند.وقتی که رقم دهگان 5 بیشتر است، خارج قسمت امتحانی (اگر نادرست باشد) باید به عدد کوچک تر گرد شود یا با به کارگیریروش ظاهری، باید آن را بزرگ تر انتخاب کنیم.وقتی که رقم دهگان کوچک تر از 4 است، خارج قسمت امتحانی (ر صورت نادرست بودن) باید در هر دو روش بزرگ تر از قبل انتخاب شود.