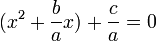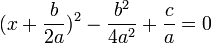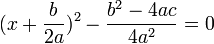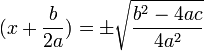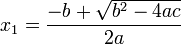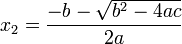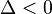آموزش یافتن ریشه معادلات درجه اول و درجه دوم
برای مثال ریشه های معادله ی فرضی

نسبت به محور xها در واقع مجموعه ای از نقاط اشتراک نمودار معادله با محور xها می باشد و چون آن نقاط بر روی محور xها واقع می باشند یعنی دارای عرض صفر هستند، بدین منظور باید مقدار x را در معادله ای که عرض (y) آن صفر است درآوریم.
حل معادله درجه اول
برای پیدا کردن ریشههای x یک معادله ی درجه اول باید مقدار x را از حالت کلی معادلات درجه اول به دست آوریم. حالت کلی معادلات درجه اول برابر  می باشد که در آن
می باشد که در آن  عرض اصلی،
عرض اصلی، 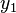 عرض اولیه، m شیب نمودار و x متغیر طول نمودار می باشد، همچنین در اکثر منابع شکل اصلی معادلات درجه اول به صورت
عرض اولیه، m شیب نمودار و x متغیر طول نمودار می باشد، همچنین در اکثر منابع شکل اصلی معادلات درجه اول به صورت 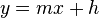 نمایش داده می شود که در آن h همان عرض اولیه است که به اختصار از کلمه height استفاده می شود
نمایش داده می شود که در آن h همان عرض اولیه است که به اختصار از کلمه height استفاده می شود
روش حل معادلات درجه اول بدین گونه است:

با حل معادله ی فوق به ترتیب زیر مقدار x را بدست می آوریم:
چون می خواهیم نقاط تلاقی نمودار با محور xها را پیدا کنیم عرض آن (y) را برابر صفر قرار می دهیم و داریم:

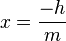
و می بینیم که مقدار x همواره برابر است با حاصل تقسیم عرض از مبداً معادله بر شیب آن. بنابراین هنگامی که عرض از مبداً معادله صفر باشد ریشه معادله نیز صفر است و نمودار معادله از مبداً مختصات خواهد گذشت.
حل معادلات درجه دوم
همانند حل معادلات درجه اول برای پیدا کردن نقاط تقاطع معادله با محور xها صورت کلی معادلات درجه دوم را نوشته و عرض آن (y) را برابر صفر قرار می دهیم، پس داریم:
با حل معادله ی فوق مقادیر x را بدست می آوریم، توجه کنید که a برابر با صفر نمی تواند باشد چون در این صورت معادله از نوع درجه اول می شود. پس با شرط a≠0 معادله را حل می کنیم:
اگر ضرب چند عبارت برابر با صفر باشد پس حداقل یکی از آنها صفر است، از آنجا که a بنا بر شرط اولیه نمی تواند صفر باشد پس عبارت داخل پرانتز صفر می باشد، پس داریم:
برای حل معادله آن را تبدیل به مربع کامل می کنیم:
حالا از طرفین معادله جذر می گیریم تا مقدار x را درآوریم:
در نتیجه معادله دارای 2 ریشه زیر می باشد:
معمولاً عبارتطبق قضیه تثلیث دلتا می تواند مقادیر زیر را اختیار کند:
1 -2 -
که در آن صورت فاصله ی بین دو ریشه صفر است، پس هر دو جواب معادله یکی هستند و معادله اصطلاحاً ریشه مضاعف دارد
3 -
- لینک منبع
تاریخ: جمعه , 12 اسفند 1401 (21:42)
- گزارش تخلف مطلب